別に特に内容がなくたって今日の数式を書いてもいいはずです。
今日の数式:階段関数(ヘヴィサイド関数)とその微分
階段関数(ヘヴィサイド関数, Heaviside Step Function)$\Theta(x)$ は
$$
\Theta(x) = \begin{cases}
0 & x < 0 \\ \frac{1}{2} & x=0 \\ 1 & x > 0
\end{cases}
$$
で定義され、
その微分 $\frac{ d\Theta(x)}{dx}$ として
ディラックのデルタ関数 $\delta(x)$ を定義できます。
$$
\delta(x) = \frac{d\Theta(x)}{dx}
$$
階段関数とディラックのデルタ関数のグラフは以下のようになります。
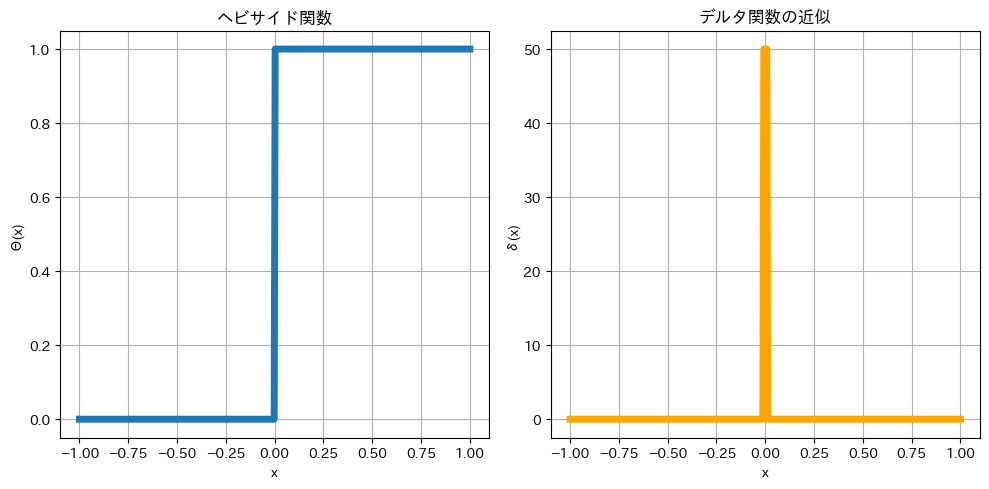
階段関数とデルタ関数
具体例:統計力学
$N$ 個の粒子が3次元空間上を運動していることを考えます。
この時、とりうるすべての状態は
$$\Gamma = (\mathrm{r}_1, \dots , \mathrm{r}_N , \mathrm{p}_1, \dots , \mathrm{p}_N) \in \mathbb{R}^{6N}$$
で表せます。位置と運動量の $6N$ 次元の空間のことを相空間と呼びます(位相空間とも)。
相空間の”体積” $\Omega = \int_{H\le E} d\Gamma$ は、階段関数を用いて
$$
\begin{align*}
\Omega(E,k,N) &= \int_{H\le E} d\Gamma \\
&=\int\Theta\bigg(E-H(\Gamma \,;k,N)\bigg) \, d\Gamma
\end{align*}
$$
と表せます。
たとえば巨視的な仕事を求めたいとき、
$$\begin{align*}
\frac{\partial \Omega}{\partial k}
&= \frac{\partial }{\partial k}\int\Theta\bigg(E-H(\Gamma \,;k,N)\bigg) \, d\Gamma &(\text{先ほど書いた}\Omega)\\
&= \int -\delta\bigg( E – H(\Gamma;k,N)\bigg)\frac{\partial H}{\partial k} \,d\Gamma &(階段関数 \Theta の微分と連鎖律)\\
&= -\int\Sigma(E,k,N) \,\rho^{mc}_{E,k,N} (\Gamma) \frac{\partial H}{\partial k}
\end{align*}$$
のような式変形が出てきました。
最後はミクロカノニカル分布の定義
$$\rho^{mc}_{E,k,N}=\frac{\delta( E – H(\Gamma;k,N))}{\Sigma(E,k,N)}$$
を用いています。
参考文献
注:以下はアマゾンのアソシエイトリンクとなっています。

物理数学の復習に使います。
解説が丁寧で、どこで間違ったのかすぐにわかります。

LaTeXについて知りたいすべてが書かれている本です。
この本とインターネットがあれば、LaTeXで必要なことはほぼ乗っています。
コメント