目的:前の記事の内容は概ね正しいですが、変数変換の扱い、用語の厳密性、”再生性” の仮定の明示、改善の余地がありました。ここではそれぞれ整理し、必要な補足を入れて示します。
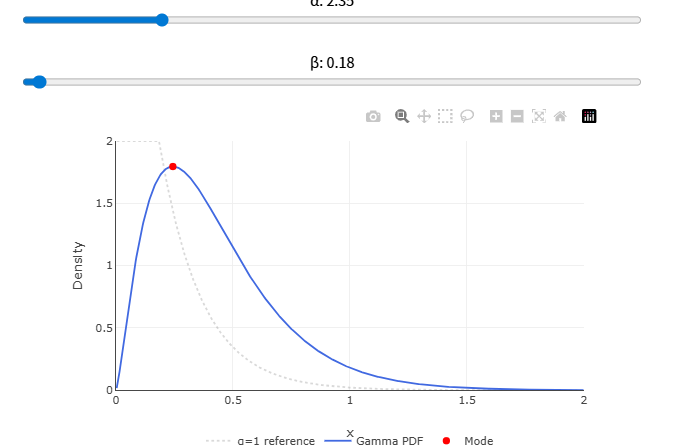
1. ガンマ分布の定義(形状・尺度)
パラメータ \(\alpha>0\)(形状: shape)と \(\beta>0\)(尺度: scale)を用いる表記で、ガンマ分布の確率密度関数は
\[ f_{\alpha,\beta}(x)=\begin{cases}\dfrac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\,x^{\alpha-1}\,e^{-x/\beta}, & x>0,\\[6pt] 0,&\text{それ以外.}\end{cases}\]
2. 期待値と分散の導出
まずは期待値を求めます。定義は
\[E[X]=\int_0^{\infty} x f_{\alpha,\beta}(x)\,dx\]
でした。確率密度関数\(f_{\alpha,\beta}(x)\)の定義より、
\begin{aligned} E[X]&=\frac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\int_0^{\infty} x\,x^{\alpha-1}e^{-x/\beta}\,dx \\ &=\frac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\int_0^{\infty} x^{\alpha} e^{-x/\beta}\,dx. \end{aligned}
と変形できます。\(t=x/\beta\) の置換を用いると(\(x=\beta t\), \(dx=\beta dt\))
\begin{aligned} E[X]&=\frac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\int_0^{\infty} (\beta t)^{\alpha} e^{-t}\,\beta dt \\ &=\frac{\beta^{\alpha+1}}{\Gamma(\alpha)\,\beta^{\alpha}}\int_0^{\infty} t^{\alpha} e^{-t}\,dt \\ &=\beta\frac{\Gamma(\alpha+1)}{\Gamma(\alpha)}=\beta\alpha. \end{aligned}
したがって \(E[X]=\alpha\beta\)となります。
次に分散\(\mathrm{Var}(X)=E[X^2]-E[X]^2\)を求めます。そのためにはまず \(E[X^2]\) を求めます。先ほどと同様、確率密度関数\(f_{\alpha,\beta}(x)\)の定義より
\begin{aligned} E[X^2]&=\frac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\int_0^{\infty} x^{\alpha+1} e^{-x/\beta}\,dx \\ &=\frac{\beta^{2}}{\Gamma(\alpha)}\Gamma(\alpha+2)=\beta^{2} (\alpha+1)\alpha /\Gamma(\alpha) \cdot \Gamma(\alpha) \\ &=\beta^{2} \alpha(\alpha+1). \end{aligned}
よって
\[(\mathrm{Var}(X)=\beta^{2}\alpha(\alpha+1)-(\alpha\beta)^2=\alpha\beta^{2}\]
3. 標準正規の二乗がカイ二乗分布になる(変数変換を厳密に)
標準正規分布 \(Z\sim N(0,1)\) の確率密度は
\[\varphi(z)=\dfrac{1}{\sqrt{2\pi}}e^{-z^2/2}\]
\(X=Z^2\) と変数変換します。\((X\ge0)\)
この変換に対して変換公式の一般形を使います。もし \(g\) が可逆でない場合、元の変数の各逆像を足し合わせる必要があります。(具体的には、\(x>0\) に対して \(z=\sqrt{x}\) と \(z=-\sqrt{x}\) の二つ)
\[ f_X(x)=\sum_{z:\,g(z)=x} f_Z(z)\left|\frac{dz}{dx}\right|. \]
ここで \(g(z)=z^2\)より \(dz/dx=\dfrac{1}{2\sqrt{x}}\)(正の平方根側で計算する)なので、両方の逆像について和をとると:
\begin{aligned} f_X(x)&=f_Z(\sqrt{x})\left|\frac{d}{dx}(\sqrt{x})\right|+f_Z(-\sqrt{x})\left|\frac{d}{dx}(-\sqrt{x})\right| \\ &=\frac{1}{\sqrt{2\pi}}e^{-x/2}\cdot\frac{1}{2\sqrt{x}}+\frac{1}{\sqrt{2\pi}}e^{-x/2}\cdot\frac{1}{2\sqrt{x}} \\ &=\frac{1}{\sqrt{2\pi}}e^{-x/2}\cdot\frac{1}{\sqrt{x}} \\ &=\frac{1}{2^{1/2}\Gamma(1/2)}x^{1/2-1}e^{-x/2} \end{aligned}
この右辺はガンマ分布の確率密度関数において、形状 \(\alpha=\tfrac{1}{2}\)、尺度 \(\beta=2\) としたものに一致します。よって \(Z^2\sim\Gamma(1/2,2)\)です。
一般に、独立な標準正規 \(Z_1,\dots,Z_k\) の二乗和 \(\sum_{i=1}^k Z_i^2\) はカイ二乗分布 \(\chi^2_k\) に従い、これはガンマ分布 \(\Gamma(k/2,2)\) と等価となります。
4. ガンマ分布の再生性(再現性)の証明と条件
独立な \(X_1\sim\Gamma(\alpha_1,\beta)\) と \(X_2\sim\Gamma(\alpha_2,\beta)\) について、
それらを加えた和 \(X_1+X_2\) も \(\Gamma(\alpha_1+\alpha_2,\beta)\) に従うことを示します。
証明(ラプラス変換/モーメント母関数を使う簡潔な方法):ガンマ分布のラプラス変換(MGF に類似)を考えます。\(X\sim\Gamma(\alpha,\beta)\) のラプラス変換は
\[ L_X(t)=E[e^{-tX}]=(1+\beta t)^{-\alpha},\quad t>-1/\beta. \]
独立性より、和のラプラス変換は積になります
\[ L_{X_1+X_2}(t)=L_{X_1}(t)L_{X_2}(t)=(1+\beta t)^{-\alpha_1-\alpha_2}. \]
右辺は \(\Gamma(\alpha_1+\alpha_2,\beta)\) のラプラス変換となっているので、和もガンマ分布で形状パラメータが加法的に足される。
5. カイ二乗(自由度 \(n\))の確率収束:\(\chi^2_n/n\to1\) 対数の弱法則
独立な標準正規 \(Z_1,\dots,Z_n\) に対して
\[Y_n=\frac{1}{n}\sum_{i=1}^n Z_i^2\to 1\quad\text{(確率収束)}.
\]
証明(Chebyshev を用いる弱法則に相当):
- 各 \(W_i=Z_i^2\) は同分布で、期待値 \(E[W_i]=1\)、分散 \(\mathrm{Var}(W_i)=2\)(カイ二乗 1 自由度の性質)。
- 和の期待値と分散は
\[E\left[\sum_{i=1}^n W_i\right]=n,\qquad \mathrm{Var}\left(\sum_{i=1}^n W_i\right)=n\cdot 2=2n.
\] - したがって
\[\mathrm{Var}(Y_n)=\mathrm{Var}\left(\frac{1}{n}\sum_{i=1}^n W_i\right)=\frac{2n}{n^2}=\frac{2}{n}.
\] - Chebyshev の不等式より、任意の \(\varepsilon>0\) に対して
\[P(|Y_n-1|\ge\varepsilon)\le\frac{\mathrm{Var}(Y_n)}{\varepsilon^2}=\frac{2}{n\varepsilon^2}\to 0\quad(n\to\infty).
\]

コメント