1. ガンマ分布の定義(密度関数)
パラメータを形状母数 \( \alpha>0 \) と尺度母数 \( \beta>0 \) とするガンマ分布 \( \Gamma(\alpha,\beta) \) の確率密度関数は次のように定義されます。
f_{\alpha\beta}(x)=
\begin{cases}
\dfrac{1}{\Gamma(\alpha)\,\beta^{\alpha}} \; x^{\alpha-1} e^{-x/\beta}, & x>0,\\[6pt]
0, & x\le 0,
\end{cases}
\]
ここで正規化定数\(\dfrac{1}{\Gamma(\alpha)\,\beta^{\alpha}}\) に含まれる\( \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}\,dt \) はガンマ関数です。
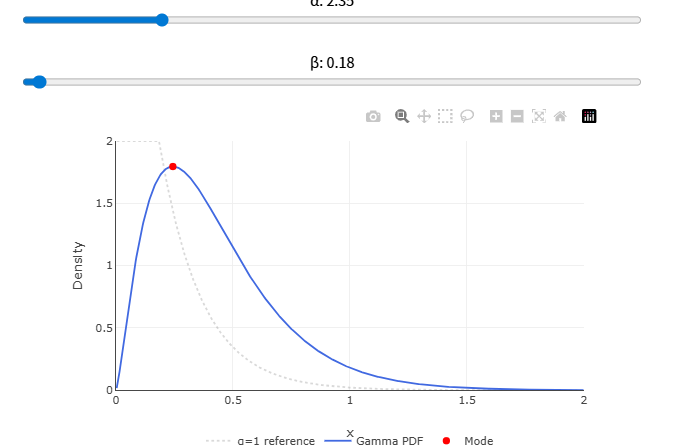
\(\alpha\) は分布の形(小さいと裾が重い・尖った形、大きいと山に近い)、\(\beta\) は尺度(単位)の役割を持ちます。図を動かしてみてください。
1.1 正規化定数の確認(密度が積分して1になること)
説明(ステップ):
- 変数変換 \( y=x/\beta \) を使うと
\[
\int_0^\infty x^{\alpha-1} e^{-x/\beta}\,dx
= \beta^\alpha \int_0^\infty y^{\alpha-1} e^{-y}\,dy
= \beta^\alpha \Gamma(\alpha).
\] - よって密度の分母にある \( \Gamma(\alpha)\beta^\alpha \) で割ると全積分は1になります。\(\square\)
2. ガンマ関数とベータ関数の関係
ガンマ関数 \( \Gamma(z) \) は上で定義した積分で、ベータ関数は
B(x,y)=\int_0^1 t^{x-1}(1-t)^{y-1}\,dt \quad (x,y>0).
\]
ガンマ関数とベータ関数は次の関係を持ちます:
B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}.
\]
3. ガンマ分布の期待値と分散(計算と性質)
目標: \(X\sim\Gamma(\alpha,\beta)\) のとき \(E[X]=\alpha\beta\), \(\mathrm{Var}(X)=\alpha\beta^2\) を示す。
3.1 期待値の計算
- 定義より
\[
E[X]=\int_0^\infty x \cdot \frac{1}{\Gamma(\alpha)\beta^{\alpha}} x^{\alpha-1} e^{-x/\beta}\,dx
=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\int_0^\infty x^{\alpha} e^{-x/\beta}\,dx.
\] - 変数変換 \( y=x/\beta \Rightarrow x=\beta y, dx=\beta dy \) を使うと
\[
\int_0^\infty x^{\alpha} e^{-x/\beta}\,dx
=\beta^{\alpha+1}\int_0^\infty y^{\alpha} e^{-y}\,dy
=\beta^{\alpha+1}\Gamma(\alpha+1).
\] - ガンマ関数の性質 \( \Gamma(\alpha+1)=\alpha\Gamma(\alpha) \) を使い、
\[
E[X]=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\cdot \beta^{\alpha+1}\Gamma(\alpha+1)
=\beta\cdot \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)}=\beta\alpha.
\]
3.2 分散の計算
- \[
E[X^2]=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\int_0^\infty x^{\alpha+1} e^{-x/\beta}\,dx
=\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\beta^{\alpha+2}\Gamma(\alpha+2).
\] - \(\Gamma(\alpha+2)=(\alpha+1)\alpha\Gamma(\alpha)\) より
\[
E[X^2]=\beta^2\alpha(\alpha+1).
\] - したがって
\[
\operatorname{Var}(X)=E[X^2]-\big(E[X]\big)^2=\beta^2\alpha(\alpha+1)-(\beta\alpha)^2=\alpha\beta^2.
\]
まとめ:\(E[X]=\alpha\beta,\;\; \operatorname{Var}(X)=\alpha\beta^2.\)
4. 再生性(再生性とは何か・どのように示されるか)
「再生性(再生性)」とは、同じタイプの分布の独立な確率変数の和が同種の分布(ただしパラメータは変わる)となる性質を指します。ガンマ分布は次の再生性を持ちます:
「もし \(X_1,\dots,X_n\) が独立で \(X_i\sim\Gamma(\alpha_i,\beta)\) (**同じ尺度** \(\beta\) を持つ)ならば、
\[
S=\sum_{i=1}^n X_i \sim \Gamma\Big(\sum_{i=1}^n \alpha_i,\; \beta\Big).
\]」
4.1 証明(モーメント母関数 を使う)
- ガンマ分布のモーメント母関数(MGF) \(M_X(t)=E[e^{tX}]\) を計算すると(収束領域 \(t<1/\beta\)): \[ M_X(t)=\int_0^\infty e^{tx}\frac{1}{\Gamma(\alpha)\beta^{\alpha}} x^{\alpha-1} e^{-x/\beta}\,dx =\frac{1}{\Gamma(\alpha)\beta^{\alpha}}\int_0^\infty x^{\alpha-1} e^{-x(1/\beta – t)}\,dx. \] ここで \(1/\beta – t>0\) を仮定すると、変換で
\[
M_X(t)=(1-\beta t)^{-\alpha}.
\] - 独立性より \(M_S(t)=\prod_{i=1}^n M_{X_i}(t)=\prod_{i=1}^n (1-\beta t)^{-\alpha_i}=(1-\beta t)^{-\sum_i\alpha_i}\)。
- したがって \(S\) の MGF はガンマ分布 \( \Gamma(\sum\alpha_i,\beta) \) の MGF と一致するので分布が同定され、証明完了。\(\square\)
4.2 注意点
再生性が成り立つためには 尺度パラメータ \(\beta\) が共通 である必要があります。形状母数 \(\alpha\) は足し合わせて新しい形状母数になります。
5. 指数分布の場合(独立同分布の和)
指数分布はガンマ分布の特殊例です。尺度 \(\beta\) を持つ指数分布は \( \Gamma(1,\beta) \) と表せます。従って
\(X_1,\dots,X_n\) が互いに独立で \(X_i\sim\mathrm{Exp}(\beta)=\Gamma(1,\beta)\) ならば
\[
S=\sum_{i=1}^n X_i \sim \Gamma(n,\beta).
\]
期待値は \(E[S]=n\beta\)、分散は \(\operatorname{Var}(S)=n\beta^2\) です。
6. カイ二乗分布とは(定義とガンマ分布との関係)
標準正規分布 \(Z\sim N(0,1)\) に対して \(Z^2\) を考えると、これはガンマ分布の特別な形になります。一般に自由度 \(k\) のカイ二乗分布 \( \chi^2_k \) は独立な標準正規 \(Z_1,\dots,Z_k\) の二乗和
\chi^2_k \equiv \sum_{i=1}^k Z_i^2
\]
で定義されます。
6.1 標準正規の二乗がガンマ分布になること(変数変換で示す)
- 標準正規の密度は
\[
f_Z(z)=\frac{1}{\sqrt{2\pi}}e^{-z^2/2}.
\]
変数変換 \(X=Z^2\) (\(z=\pm\sqrt{x}\))を使うと \(x>0\) に対して
\[
f_X(x)=\frac{1}{\sqrt{2\pi}}\cdot \frac{1}{2\sqrt{x}}(e^{-x/2}+e^{-x/2})
=\frac{1}{\sqrt{2\pi}} \frac{1}{\sqrt{x}} e^{-x/2}.
\] - 右辺を整理すると
\[
f_X(x)=\frac{1}{2^{1/2}\Gamma(1/2)} x^{1/2-1} e^{-x/2},
\]
なぜなら \(\Gamma(1/2)=\sqrt{\pi}\) だからです。 - これはガンマ分布 \( \Gamma(\alpha=\tfrac12,\;\beta=2) \) の密度と一致します。よって \(Z^2\sim\Gamma(1/2,2)\) です。
6.2 一般の自由度 k の場合
\(k\) 個の独立な \(Z_i^2\)(それぞれ \(\Gamma(1/2,2)\))の和は、再生性より
\[
\chi^2_k=\sum_{i=1}^k Z_i^2 \sim \Gamma\Big(\frac{k}{2},\;2\Big).
\]
これがよく知られた対応関係です:カイ二乗分布はガンマ分布の特殊ケース(形状 \(=k/2\)、尺度 \(=2\))。
7. 大数の法則・確率収束とカイ二乗分布
ここでは「大数の法則(Law of Large Numbers)」と「確率収束」を使ってカイ二乗分布から導ける簡潔な事実を示します。
7.1 カイ二乗の平均は1に収束する(標準化して見る)
考える対象:自由度 \(n\) のカイ二乗確率変数 \(Y_n\sim\chi^2_n\)。期待値と分散は次の通り:
E[Y_n]=n,\qquad \operatorname{Var}(Y_n)=2n.
\]
(これはガンマ表現 \( \Gamma(n/2,2) \) から \(E= (n/2)\cdot2=n\), \(\mathrm{Var}=(n/2)\cdot 2^2 =2n\) として得られます)
7.2 確率収束の証明(Chebyshev を使う簡単な方法)
- 標準化した平均 \(\dfrac{Y_n}{n}\) の期待値と分散を計算:
\[
E\!\left[\frac{Y_n}{n}\right]=1,\qquad
\operatorname{Var}\!\left(\frac{Y_n}{n}\right)=\frac{2n}{n^2}=\frac{2}{n}.
\] - Chebyshev の不等式より、任意の \(\varepsilon>0\) に対して
\[
P\left(\left|\frac{Y_n}{n}-1\right|\ge\varepsilon\right) \le \frac{\operatorname{Var}(Y_n/n)}{\varepsilon^2}=\frac{2}{n\varepsilon^2}.
\] - 右辺は \(n\to\infty\) で0に収束するので、
\[
\frac{Y_n}{n} \xrightarrow{p} 1
\]
すなわち確率収束(in probability)で 1 に収束する。これは弱法則の一例として解釈できます。
解釈:自由度 \(n\) のカイ二乗変数を自由度で割ると、その値は大きな \(n\) で 1 のまわりに集中する(確率的に)。これは中心極限定理や大数の法則的なふるまいと整合します。
8. 付録:別の証明法 — 畳み込みでの再生性(直接的計算)
MGF を使う方法の代わりに、畳み込み積分とベータ関数を使って再生性を示すこともできます(同じ尺度 \(\beta\) が前提)。ここでは \( \Gamma(\alpha_1,\beta) \) と \( \Gamma(\alpha_2,\beta) \) の和が \( \Gamma(\alpha_1+\alpha_2,\beta) \) になることのスケッチを示します。
- 畳み込みとして
\[
f_{X+Y}(s)=\int_0^s f_X(x) f_Y(s-x)\,dx.
\] - 各密度を代入し、共通因子を整理すると
\[
f_{X+Y}(s)=\frac{s^{\alpha_1+\alpha_2-1}}{\Gamma(\alpha_1)\Gamma(\alpha_2)\beta^{\alpha_1+\alpha_2}}
\int_0^1 u^{\alpha_1-1}(1-u)^{\alpha_2-1}\,du.
\]
ここで \(u=x/s\) の変換を使いました。 - 中の積分はベータ関数 \(B(\alpha_1,\alpha_2)=\dfrac{\Gamma(\alpha_1)\Gamma(\alpha_2)}{\Gamma(\alpha_1+\alpha_2)}\) なので、最終的に
\[
f_{X+Y}(s)=\frac{1}{\Gamma(\alpha_1+\alpha_2)\beta^{\alpha_1+\alpha_2}}s^{\alpha_1+\alpha_2-1}e^{-s/\beta},
\]
つまり \( \Gamma(\alpha_1+\alpha_2,\beta) \) の密度に一致します。これで再生性を示せます。
9. まとめ
- ガンマ分布は形状 \(\alpha\)、尺度 \(\beta\) を持つ連続分布で密度は \(\dfrac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}\)。(正規化はガンマ関数で示せる)
- 期待値・分散: \(E[X]=\alpha\beta,\ \operatorname{Var}(X)=\alpha\beta^2\)。ガンマ関数の性質 \(\Gamma(\alpha+1)=\alpha\Gamma(\alpha)\) を用いて導出する。
- 再生性:同じ尺度 \(\beta\) を持つ独立なガンマ分布の和は再びガンマ分布(形状は足し合わせる)。MGF または畳み込み+ベータ関数で示せる。
- 指数分布は \(\Gamma(1,\beta)\)。独立同分布の和は \(\Gamma(n,\beta)\)。
- カイ二乗分布はガンマ分布の特殊形で、自由度 \(k\) のとき \( \chi^2_k\sim\Gamma(k/2,2)\)。これは標準正規の二乗和として得られる。
- 大数の法則的観点:\(Y_n\sim\chi^2_n\) に対して \(Y_n/n \xrightarrow{p} 1\)。期待値と分散から Chebyshev を使えば簡潔に示せる。
10. メモ
– ガンマ分布は待ち時間・到着過程・ベイズ統計などで広く使われます。
– パラメータ表記には形状-尺度 \((\alpha,\beta)\) の他に形状-率(rate)表記 \((\alpha,\lambda)\)(密度に \(e^{-\lambda x}\))を用いることがあり、変換 \(\lambda=1/\beta\) に注意してください。
– 証明はすべて丁寧に書くと積分計算とガンマ関数・ベータ関数の基本関係を使うことに帰着します。
今日の数式:ガンマ関数・ベータ関数
\mathrm B (\alpha,\beta) \stackrel{\mathrm{def}}{=} & \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} dx \ \ \ &(\alpha,\beta >0)
\end{align}$$
任意の\(\alpha,\beta>0\)に対して、次が成立します。
\Gamma(\alpha+1) = \alpha\Gamma(\alpha), \ \ & \Gamma(1)=1 \\
\text{特に、}\\
\Gamma(n+1)=n!\ \ &(n\in\mathbb{N})
\end{align}$$
2. $$\mathrm B (\alpha,\beta) = \mathrm B (\beta,\alpha) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$$
3. $$\mathrm B (\alpha,\beta) = 2\int_0^{\frac{\pi}{2}}(\sin^{2\alpha-1}\theta \ \cos^{2\beta-1}\theta )\ d\theta$$
4. $$\mathrm B (\frac{1}{2},\frac{1}{2}) = \pi,\ \ \Gamma(\frac{1}{2})=\sqrt\pi$$

コメント